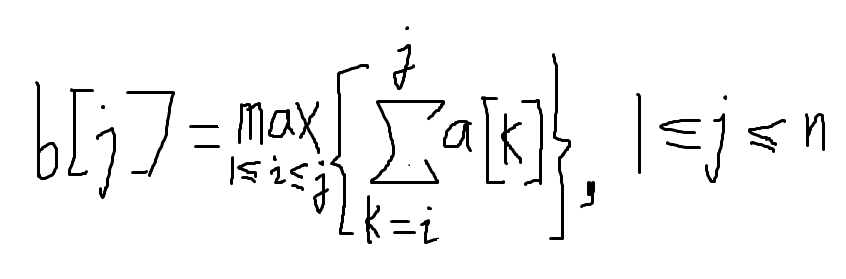

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| public class Test6 {
static int MAX = 10;
static int[] a = {0, -2, 11, -4, 13, -5, -2};
static int N = 6;
public static void main(String[] args) {
int maxSum = 0;
for (int i = 1; i <= N; i++) {
for (int j = 1; j + i - 1 <= N; j++) {
int end = i + j - 1;
if (end <= N) {
int temp = 0;
for (int k = j; k <= end; k++) {
temp += a[k];
}
maxSum = Math.max(maxSum, temp);
}
}
}
System.out.println(maxSum);
}
}
|
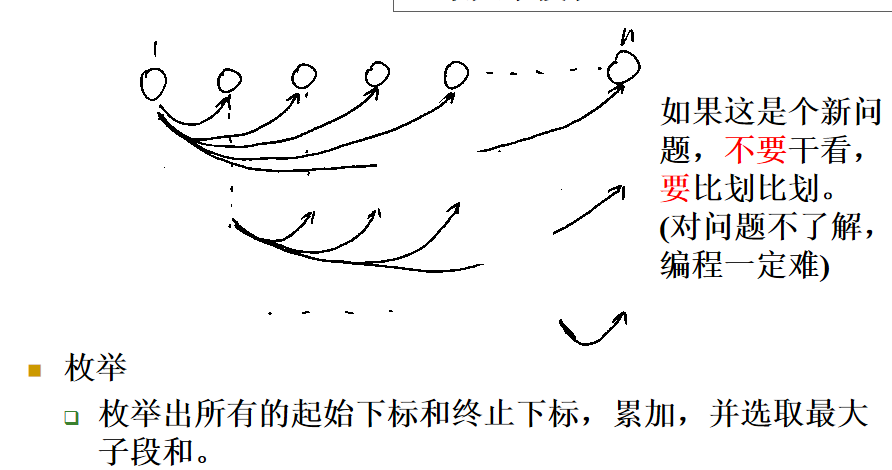
充分利用已经得到的结果,避免重复计算,节省计算时间
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| public class Test6 {
static int MAX = 10;
static int[] a = {0, -2, 11, -4, 13, -5, -2};
static int[][] dp = new int[MAX][MAX];
static int N = 6;
public static void main(String[] args) {
int maxSum = 0;
for (int i = 1; i <= 6; i++) {
dp[1][i] = a[i];
}
for (int i = 2; i <= N; i++) {
for (int j = 1; j <= N; j++) {
int k = i + j - 1;
if (k <= N) {
dp[i][j] = dp[i - 1][j] + a[k];
if (dp[i][j] > maxSum) {
maxSum = dp[i][j];
}
}
}
}
System.out.println(maxSum);
}
}
|
扫描一次整个数列的所有数值,在每一个扫描点计算以该点数值为结束点的子数列的最大和( 正数和 )。 该子数列由两部分组成:以前一个位置为结束点的最大子数列、该位置的数值。 因为该算法用到了“最佳子结构”(以每个位置为终点的最大子数列都是基于其前一位置的最大子数列计算得出), 该算法可看成动态规划的一个例子。
将长度为n的目标序列存储在一个数组中,设为a。设数组b为如下
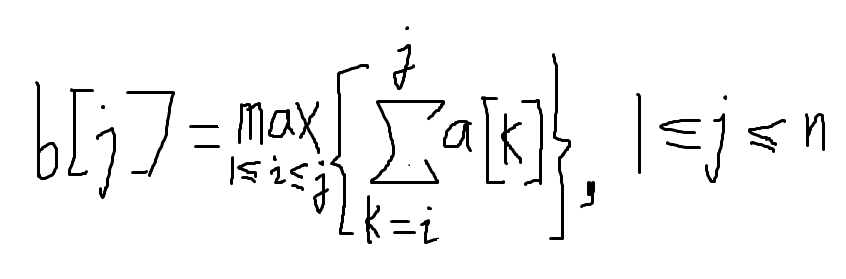
当b[j-1] > 0时 b[j] = b[j-1] + a[j],否则b[j] = a[j]。由此可得计算b[j]的动态规划递归方程
b[j] = max{b[j - 1] + a[j],a[j]}, 1 <= j <= n
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| public class Test6 {
static int MAX = 10;
static int[] a = {0, -2, 11, -4, 13, -5, -2};
static int N = 6;
public static void main(String[] args) {
int sum = 0;
int this_sum = 0;
for (int i = 1; i <= N; i++) {
if (this_sum > 0)
this_sum = this_sum + a[i];
else
this_sum = a[i];
sum = Math.max(this_sum, sum);
}
System.out.println(sum);
}
}
|
参考文章