发表更新数据结构和算法31 分钟读完 (大约4680个字)

动态规划

基本思想

动态规划方法的基本思想是，把求解的问题分成许多阶段或多个子问题，然后按顺序求解各子问题。最后一个子问题就是初始问题的解。

由于动态规划的问题有重叠子问题的特点，为了减少重复计算，对每一个子问题只解一次，将其不同阶段的不同状态保存在一个二维数组中。

动态规划=贪婪策略+递推(降阶)+存储递推结果

  • 空间换取时间

    • 递归算法效率低的主要原因是因为进行了大量的重复计算。而动态规划的基本动机就是充分利用重叠子问题(Overlapping subproblems)。
    • 因为动态规划将以前（子问题）计算过的结果都记录下来，遇到使用子问题结果的时候只需查表。
    • 动态规划是一种用空间换取时间的方法。

因此，动态规划常常因为空间消耗太大而难以实现。

主要概念

  • 阶段：把问题分成几个相互联系的有顺序的几个环节，这些环节即称为阶段。
  • 状态：某一阶段的出发位置称为状态。通俗地说状态是对问题在某一时刻的进展情况的数学描述。
  • 决策：从某阶段的一个状态演变到下一个阶段某状态的选择。
  • 状态转移方程：根据上一阶段的状态和决策导出本阶段的状态。这就像是“递推”。
    img.png

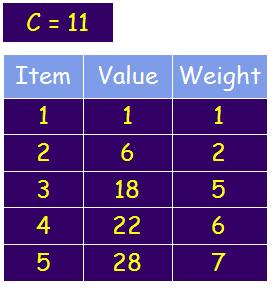
例: 数塔问题

从顶部出发，在每一结点可以选择向左走或是向右走，一直走到底层，要求找出一条路径，使路径上的数值和最大。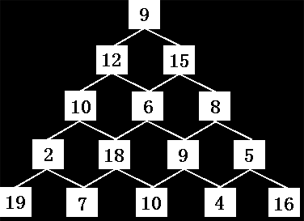
img_1.png

  • 阶段：每行就是一个阶段；
  • 状态：d[i][j]，即取第i行，第j个数能够达到的最大值；
  • 决策：取第i行第j个数，则可以有两种方案：取第i-1行第j-1个数或取第i-1行第j个数后再取第i行第j个数；
  • 状态转移方程：
    d[i][j] = max (d[i+1][j]，d[i+1][j+1]) + data[i][j]；
    表示取第i行第j个数所能达到的最大和；
1
2
3
4
5
6
7
8
9
int a[100][100], f[100][100];
int max(int i,int j,int n){
	int left,right;
	if ((i==n)||(j==n)) f[i][j] =a[i][j]; 	
    if (f[i][j] != -1) return f[i][j];
	left=max(i+1,j,n); //左边
	right=max(i+1,j+1,n); //右边
	return (f[i][j] = (left>right)? (left+a[i][j]):(right+a[i][j]));
}

适合解决的问题的性质

  • 动态规划算法的问题及决策应该具有两个性质：最优化原理、无后向性。
  1. 最优化原理(或称为最佳原则、最优子结构)；
  2. 无后向性(无后效性)：某阶段状态一旦确定以后，就不受这个状态以后决策的影响。即某状态以后的过程不会影响以前的状态，只与当前状态有关。
  • 能够体现动态规划优点的性质：
    • 子问题重叠性质；
    • 动态规划用空间换取时间，在有大量重叠子问题的时候其优势才能充分体现出来。

例：数塔问题

  • 最优化原理(最优子结构)
    9->12->10->18->10
    显然12->10->18->10也是12到最后一层的最大和……
  • 无后效性
    如，计算到12的最大和只要考虑到10的最大和与到6的最大和哪个更大，而不要考虑到10的最大和或者到6的最大和具体是哪几个数构成的。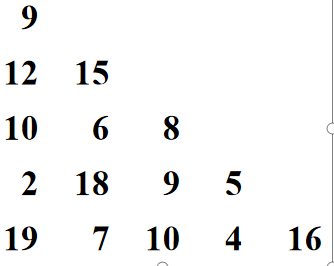
    img_3.png

    设计步骤

    设计动态规划算法的基本步骤

    设计一个标准的动态规划算法的步骤：

  1. 划分阶段；
  2. 选择状态；
  3. 确定决策并写出状态转移方程。

    实际应用当中的简化步骤：

  4. 分析最优解的性质，并刻划其结构特征。
  5. 递推地定义最优值。
  6. 以自底向上的方式或自顶向下的记忆化方法(备忘录法)计算出最优值。
  7. 根据计算最优值时得到的信息，构造问题的最优解。

例题： 数塔问题

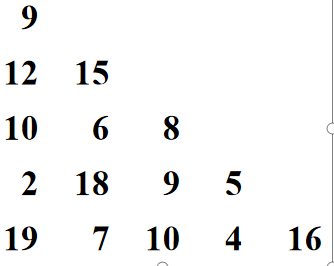
img_3.png

//从顶部出发，在每一结点可以选择向左走或是向右走，一直走到底层，要求找出一条路径，使路径上的数值和最大。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public class Test1 {
	static int[][] result = new int[5][5];

	public static int maxSum(int i, int j, int[][] data) {
		if (i == data.length - 1 || j == data.length - 1) {
			result[i][j] = data[i][j];
		}
		if (result[i][j] != 0) {
			return result[i][j];
		}
		return result[i][j] = Math.max(maxSum(i + 1, j, data), maxSum(i + 1, j + 1, data)) + data[i][j];
	}

	public static void main(String[] args) {
		int[][] data = {{9}, {12, 15}, {10, 6, 8}, {2, 18, 9, 5}, {19, 7, 10, 4, 16}};
		maxSum(0, 0, data);
		System.out.println(result[0][0]);
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
public class Test1 {
	static int[][] dp = new int[5][5];
	static int n = 5;
	public static void maxSum(int[][] data) {
		// dp初始化
		for (int i = 0; i < n; ++i) {
			dp[n - 1][i] = data[n - 1][i];
		}
		int temp_max;
		for (int i = n - 2; i >= 0; --i) {
			for (int j = 0; j <= i; ++j) {
				// 使用递推公式计算dp的值
				temp_max = Math.max(dp[i + 1][j], dp[i + 1][j + 1]);
				dp[i][j] = temp_max + data[i][j];
			}
		}
	}
	private static void printPath(int[][] data) {
		System.out.printf("最大路径： " + data[0][0] + "");
		int j = 0;
		for (int i = 1; i < 5; ++i) {
			int node_value = dp[i - 1][j] - data[i - 1][j];
			/* 如果node_value == dp[i][j]则说明下一步应该是data[i][j]；如果node_value == dp[i][j + 1]则说明下一步应该是data[i][j + 1]*/
			if (node_value == dp[i][j + 1])
				++j;
			System.out.printf("->" + data[i][j]);
		}
		System.out.println();
	}
	
	public static void main(String[] args) {
		int[][] data = {{9}, {12, 15}, {10, 6, 8}, {2, 18, 9, 5}, {19, 7, 10, 4, 16}};
		maxSum(data);
		System.out.println("最大路径和： " + dp[0][0]);

		printPath(data);
	}


}

资源分配问题

设有资源n(n为整数),分配给m个项目,gi(x)为第i个项目分得资源x(x为整数)所得到的利润。

  • 求总利润最大的资源分配方案，也就是解下列问题：

    1
    2
    max z=g1(x1)+ g2(x2)+……gm(xm)
    x1+x2+x3+……xm = n，0≤xi≤n，i=1,2,3,……,m

    函数gi(x)以数据表的形式给出。

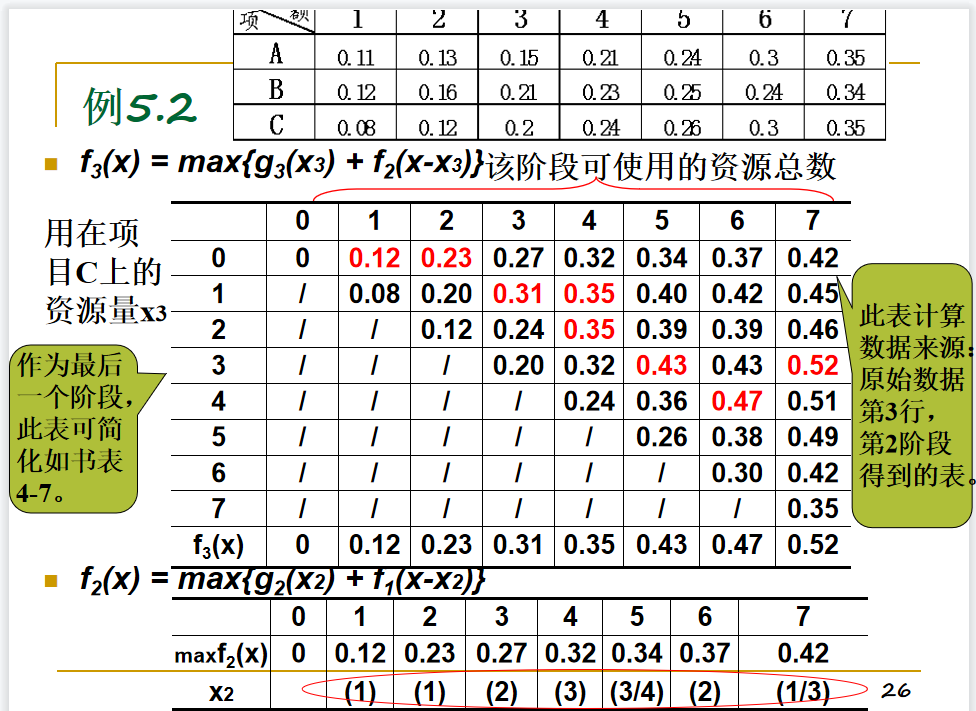
  • 例如：现有7万元投资到A，B，C 三个项目，利润见表,问题：求总利润最大的资源分配方案。
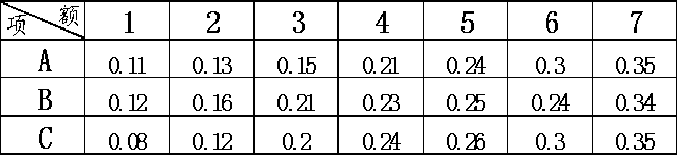
    img_4.png

  • 划分阶段或找到子问题；
    每个阶段增加一个项目，考察投资利润情况。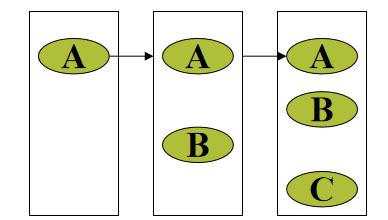
    img_5.png
    img_6.png
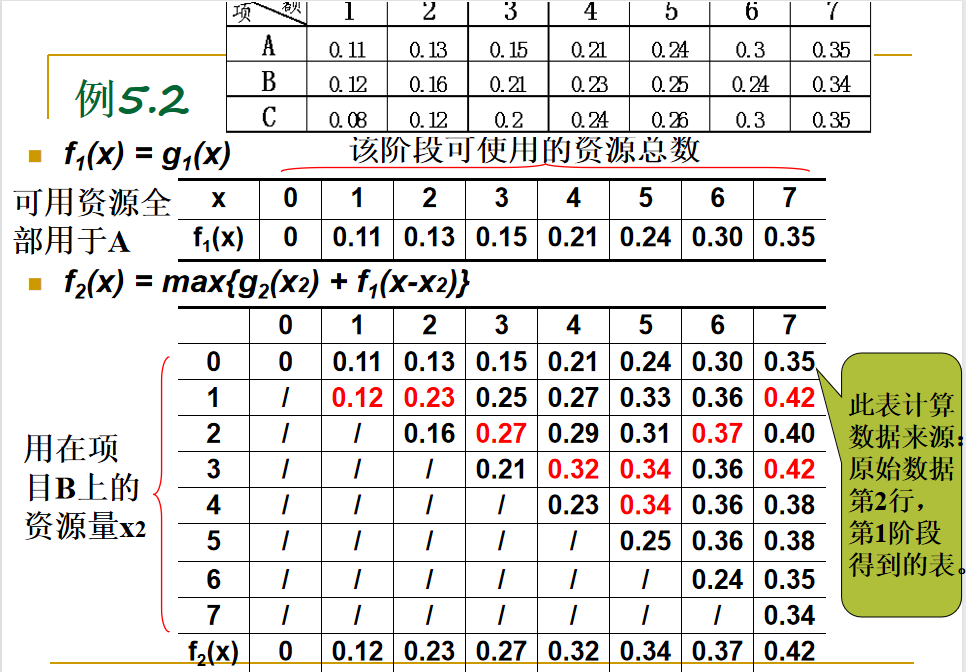
    img_7.png
    img_8.png
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60

    public class Test2 {
    	static double[][] v = {
    		{0, 0.11, 0.13, 0.15, 0.21, 0.24, 0.3, 0.35},
    		{0, 0.12, 0.16, 0.21, 0.23, 0.25, 0.24, 0.34},
    		{0, 0.08, 0.12, 0.2, 0.24, 0.26, 0.3, 0.35}};
    	static int m = 3;
    	static int n = 7;

    	public static void main(String[] args) {
    		double[] q = new double[10];  //原始数据（逐行使用）
    		double[] f = new double[10];//当前最大收益情况
    		double[] temp = new double[10]; //正在计算的最大收益
    		int[][] a = new int[10][10]; //前i个项目投资j获得最大利润时，给第i个项目分配的资源数(m*(n+1)维)
    		int[] gain = new int[10];//在不同投资数下获最大利润时第i个工程所得资源数。

    		// 全部资源用于A(第一个项目) 
    		q = f = v[0];

    		for (int j = 0; j <= n; j++) {
    			a[1][j] = j;
    		}

    		// 第二阶段： 全部资源用于两个项目
    		// 第三阶段： 全部资源用于三个项目
    		for (int k = 2; k <= m; k++) {
    			for (int j = 0; j <= n; j++) {
    				temp[j] = q[j];
    				a[k][j] = 0;
    			}
    			//赋值， 第二/三个项目的收益情况 (数组下标从0开始，故此处k-1)
    			q = v[k - 1];

    			for (int j = 0; j <= n; j++) {
    				for (int i = 0; i <= j; i++) {
    					if (f[j - i] + q[i] > temp[j]) {
    						temp[j] = f[j - i] + q[i];
    						a[k][j] = i;
    					}
    				}
    			}
    			// 更新 当前最大收益情况
    			for (int j = 0; j <= n; j++)
    				f[j] = temp[j];
    		}

    		int rest = n;
    		for (int i = m; i >= 1; i--) {
    			gain[i] = a[i][rest];
    			rest = rest - gain[i];
    		}
    		for (int i = 1; i <= m; i++) {
    			System.out.print(gain[i] + " ");

    		}
    		System.out.println((f[n]));
    	}

    }

资源分配问题二

资源分配问题是将数量一定的一种或若干种资源(原木料、资金、设备或劳动力等)合理地分配给若干个使用者,使总收益最大。

例如,某公司有3个商店A、B、C，拟将新招聘的5名员工分配给这3个商店，各商店得到新员工后每年的赢利情况如表所示,求分配给各商各多少员工才能使公司的赢利最大?
img_9.png
解析：

其实就是完全背包的变形

用dp[i][j]表示为前i个商店共分配j个人时盈利的最大值，状态转移方程如下（k表示为i商店分配的人数）：

dp[i][j] = max(dp[i][j], dp[i-1][j-k] + c[i][k])

img_10.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
package com.example.demo;

public class Test3 {
	public static void main(String[] args) {
		int[][] data = {
			{0, 3, 7, 9, 12, 13},
			{0, 5, 10, 11, 11, 11},
			{0, 4, 6, 11, 12, 12}
		};
		int m = 3;
		int n = 5;
		int[] q = new int[10];  //原始数据（逐行使用）
		int[] f = new int[10];//当前最大收益情况
		int[] temp = new int[10]; //正在计算的最大收益
		int[][] a = new int[10][10]; //前i个项目投资j获得最大利润时，给第i个项目分配的资源数(m*(n+1)维)
		int[] gain = new int[10];//在不同投资数下获最大利润时第i个工程所得资源数。

		// 只分配 A　
		// k =1
		q = data[0];
		f = data[0];

		for (int k = 2; k <= 3; k++) {

			q = data[k - 1];
			for (int j = 0; j <= n; j++) {
				temp[j] = q[j];
			}

			for (int j = 0; j <= n; j++) {
				for (int i = 0; i <= j; i++) {
					if (f[j - i] + q[i] > temp[j]) {
						temp[j] = f[j - i] + q[i];
					}
				}
			}
			for (int i = 0; i <= n; i++) {
				f[i] = temp[i];
			}
		}

		System.out.println(f[n]);
	}
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
package com.example.demo;

public class Test3 {
	static int MAX = 30;
	static int[][] c = new int[MAX][MAX];
	static int[][] dp = new int[MAX][MAX]; // dp[i][j]表示前i个车间共分配j个人
	static int[][] pnum = new int[MAX][MAX];
	static int n = 3, m = 5;

	public static void main(String[] args) {
		int[][] data = {
			{3, 7, 9, 12, 13},
			{5, 10, 11, 11, 11},
			{4, 6, 11, 12, 12}
		};
		for (int i = 1; i <= n; i++)
			for (int j = 1; j <= m; j++)
				c[i][j] = data[i - 1][j - 1];
		System.out.printf("max = %d\n", DP_source());
		print_allocate();

	}

	static int DP_source() {
		// 初始化
		for (int i = 0; i <= n; i++)
			dp[i][0] = 0;

		for (int i = 0; i <= m; i++)
			dp[0][i] = 0;

		int sel_num = 0; // 记录第i个车间分配j人时应分配的人数
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= m; j++) {
				sel_num = 0;
				// 枚举当前车间分配k人时的最大值
				for (int k = 0; k <= j; k++) {
					if (dp[i][j] < dp[i - 1][j - k] + c[i][k]) { // 更新答案

						dp[i][j] = dp[i - 1][j - k] + c[i][k];
						sel_num = k;
					}
				}
				// 循环结束后找到为前i个车间共分配j人时第i个车间应分配的人数
				pnum[i][j] = sel_num;
			}
		}

		return dp[n][m];

	}

	static void print_allocate() // 输出每个车间应分配的人数
	{
		int r, s;
		s = pnum[n][m]; // 最后一个车间应该选择的人数
		r = m - s; // 剩余人数
		for (int i = n; i >= 1; i--) {
			System.out.printf("%d 商店分配 %d 人\n", i, s);

			s = pnum[i - 1][r];
			r -= s;
		}
	}

}

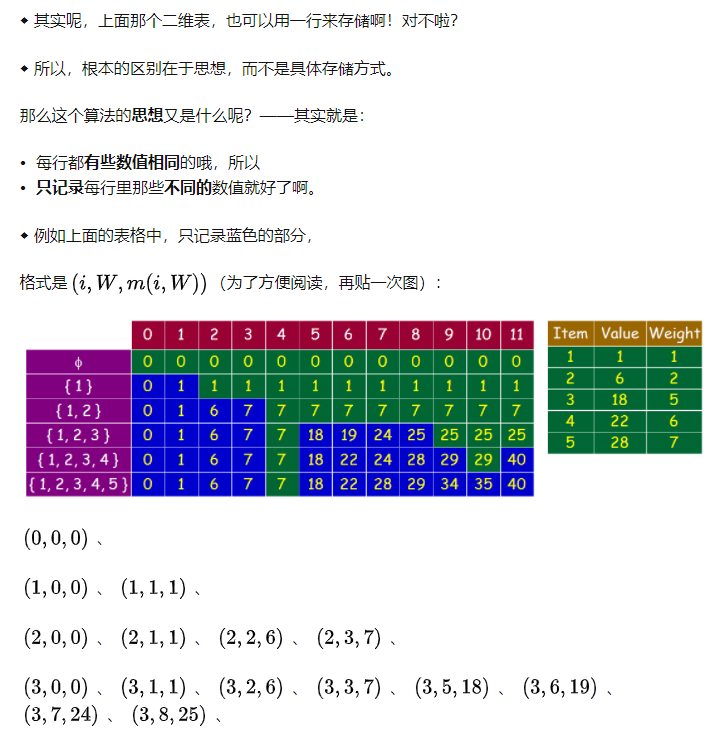
0-1背包问题（knapsack problem）

一个小偷面前有一堆（n个）财宝，每个财宝有重量w和价值v两种属性，而他的背包只能携带一定重量的财宝（Capacity），在已知所有财宝的重量和价值的情况下，如何选取财宝，可以最大限度的利用当前的背包容量，取得最大价值的财宝（或求出能够获取财宝价值的最大值）。

img_11.png

img_12.png
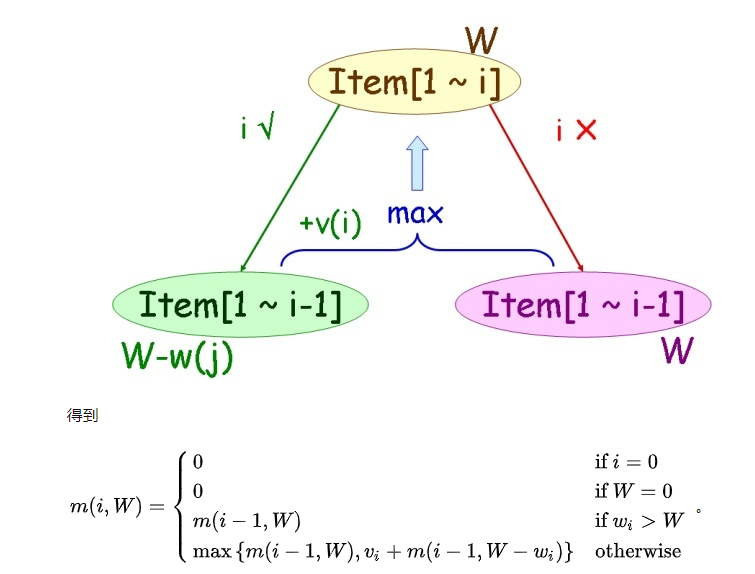
img_13.png
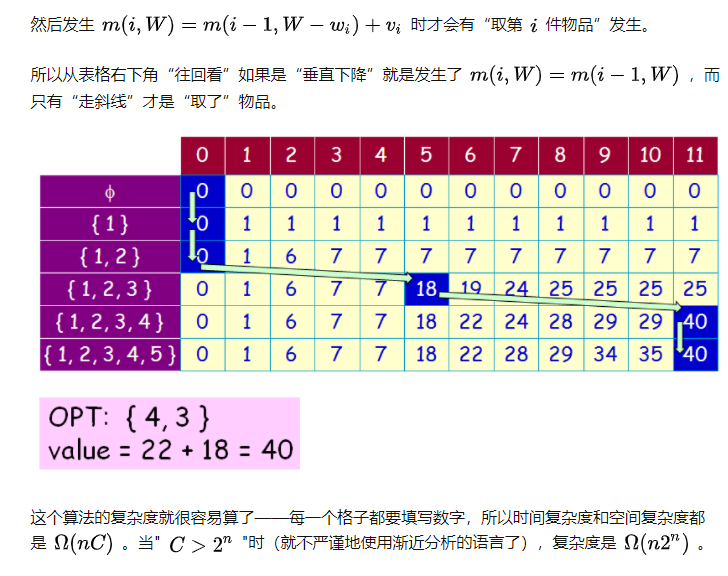
img_14.png

  • “填二维表”的动态规划方法
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    public class Test4 {
    	static int MAX = 20;
    	static int[] value = {0, 1, 6, 18, 22, 28}; //物品价值
    	static int[] weight = {0, 1, 2, 5, 6, 7}; //物品重量

    	static int[][] dp = new int[MAX][MAX]; // dp[i][j]表示容量为j, 前i个物品的总价值。
    	static int[] result = new int[MAX];  // 选择哪些物品
    	static int n = 5;//五种物品
    	static int C = 11; //背包容量

    	public static void main(String[] args) {
    		//背包容量从 1 开始递增 到 11

    		for (int i = 1; i <= 5; i++) {
    			for (int j = 1; j <= C; j++) {
    				if (weight[i] > j) {
    					dp[i][j] = dp[i - 1][j];
    				} else {
    					dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
    				}
    			}
    		}
    		System.out.println(dp[n][C]);
    	}

    }
  • 空间优化 / 填一维表”的动态规划方法

https://blog.csdn.net/weixin_41162823/article/details/87878853

dp[j] = max(dp[j], dp[j−w[i]]+v[i])

上述状态表示，我们需要用二维数组，但事实上我们只需要一维的滚动数组就可以递推出最终答案。考虑到用dp[j]来保存每层递归的值，由于我们求dp[i][j] 的时候需要用到的是dp[ i-1 ][j] 和 dp[i-1][j-w[i]] 于是可以知道，
只要我们在求 dp[j] 时不覆盖 dp[ j - w[i] ]，那么就可以不断递推至所求答案。所以我们采取倒序循环，即 v = m（m为背包总容积）伪代码如下：

1
2
3
　for i = 1..N
　　　for v = V..0
　　　　　f[ v ] = max{ f[ v ],f[ v-w[i] ]+val[ i ] };

ref: https://zhuanlan.zhihu.com/p/30959069
img_15.png

完全背包问题:

完全背包（unbounded knapsack problem）与01背包不同就是每种物品可以有无限多个：一共有N种物品，每种物品有无限多个，
第i（i从1开始）种物品的重量为w[i]，价值为v[i]。
在总重量不超过背包承载上限 W 的情况下，能够装入背包的最大价值是多少？

分析一

跟01背包一样，完全背包也是一个很经典的动态规划问题，不同的地方在于01背包问题中，每件物品最多选择一件，
而在完全背包问题中，只要背包装得下，每件物品可以选择任意多件。从每件物品的角度来说，与之相关的策略已经不再是选或者不选了，而是有取0件、取1件、取2件…直到取⌊T/Vi⌋（向下取整）件。

1
2
3
4
5
# k为装入第i种物品的件数, k <= j/w[i]
dp[i][j] = max{(dp[i-1][j-k*w[i]] + k*v[i]) }   ( 0 <= k*v[i] <= W)

dp[0][j] = 0
dp[i][0] = 0

我们通过对0/1背包的思路加以改进，就得到了完全背包的一种解法，这种解法时间复杂度为O（n^3），空间复杂度为O（n^2）。

时间优化

时间优化：根据上述 dp[i][j] 的定义，其为前 i 种物品恰好放入容量为 v 的背包的最大权值。根据上述状态转移方程可知，
我们假设的是子结果dp[i-1][j-k*w[i]] 中并没有选入第 i 种物品，所以我们需要逆序遍历（像0/1背包一样）来确保该前提；
但是我们现在考虑“加选一件第 i 种物品”这种策略时，正需要一个可能已经选入第 i 种物品的子结果dp[i-1][j-k*w[i]]，于是当我们顺序遍历时，就刚好达到该要求。这种做法，使我们省去了一层循环，即第 i 种物品放入的件数k，从而时间复杂度优化为O（n^2）。

空间优化：

正如0/1背包的空间优化，上述状态转移方程已经优化为：
dp[i][j] = max{dp[i-1][j], (dp[i][j-k*w[i]] + k*v[i]) } ( 0 <= k*v[i] <= W)

dp[i][j]表示将前i种物品装进限重为j的背包可以获得的最大价值, 0<=i<=N, 0<=j<=W

初始状态也是一样的，我们将dp[0][0…W]初始化为0，表示将前0种物品（即没有物品）装入书包的最大价值为0。那么当 i > 0 时dp[i][j]也有两种情况：

  • 不装入第i种物品，即dp[i−1][j]，同01背包；
  • 装入第i种物品，此时和01背包不太一样，因为每种物品有无限个（但注意书包限重是有限的），
    所以此时不应该转移到dp[i−1][j−w[i]]而应该转移到dp[i][j−w[i]]，即装入第i种商品后还可以再继续装入第种商品。

所以状态转移方程为
dp[i][j] = max(dp[i−1][j], dp[i][j−w[i]] + v[i]) // j >= w[i]

多重背包：

第i（i从1开始）种物品的重量为w[i]，价值为v[i]。第i种物品最多有Mi件可用
在总重量不超过背包承载上限 W 的情况下，能够装入背包的最大价值是多少？

// dp[i][j] : 前i种物品放入一个容量为 j 的背包获得的最大价值
//对于第i种物品，我们有k种选择，0 <= k <= M[i] && 0 <= k * w[i] <= j，即可以选择0、1、2…M[i]个第i种物品，所以递推表达式为：
dp[i][j] = max(dp[i][j− k * w[i]]+ k * v[i]) // 0 <= k <= M[i] && 0 <= k * w[i] <= j

视频：

参考文章

#

评论

关注我

分类

标签

Kruskal1
Object Storage1
RocketMQ1
WebSockets1
ansible7
centos11
cocos1
cubrid1
dijkstra1
docker12
docker compose6
dubbo1
elasticsearch1
filebeat1
flink1
gc1
git4
go1
graph1
hexo5
http-server1
j.u.c7
java31
java锁2
jdk1
jedis3
js1
jvm2
kafka5
kibana1
kubernetes8
leetcode10
lettuce3
linux7
logstash1
maven1
metrics3
mongodb2
mq1
mybatis-plus1
mysql6
netty3
network1
nginx13
opencv2
oracle2
pulsar1
python2
quarkus1
reactive4
redis5
spring27
spring batch1
springdoc2
springfox1
study1
tomcat1
ubuntu4
unity1
unreal1
vmware5
volatile2
webflux3
wsl7
zookeeper1
串1
二分查找2
优先队列1
动态规划8
堆1
拦截/抓包工具2
数据结构和算法10
树2
链表4

最新文章

×