2021-11-16发表2022-06-24更新数据结构和算法8 分钟读完 (大约1233个字)

深度优先搜索（DFS）

深度优先搜索是一种枚举所有完整路径以遍历所有情况的搜索方法。

从根节点开始，尽可能深的搜索每一个分支，把一个分支的结果搜索完，再去看另一个分支。
形象来说：“一条路走到底，不撞南墙不回头”。

二叉搜索树的范围和

题目描述

给定二叉搜索树的根结点 root，返回值位于范围 [low, high] 之间的所有结点的值的和。

注意哦，根节点的值大于左子树，并且根节点的值小于右子树

detail

示例1：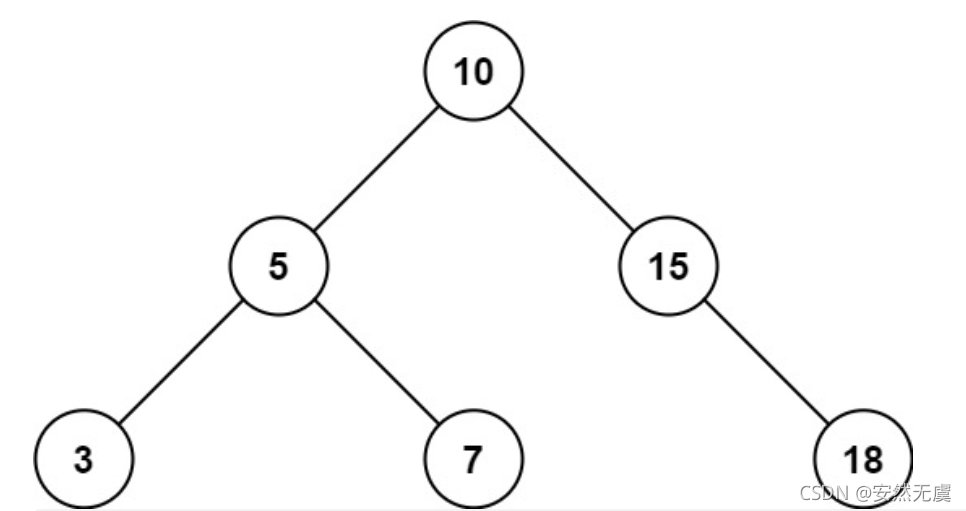

1 2	输入：root = [10,5,15,3,7,null,18], low = 7, high = 15 输出：32

示例2：

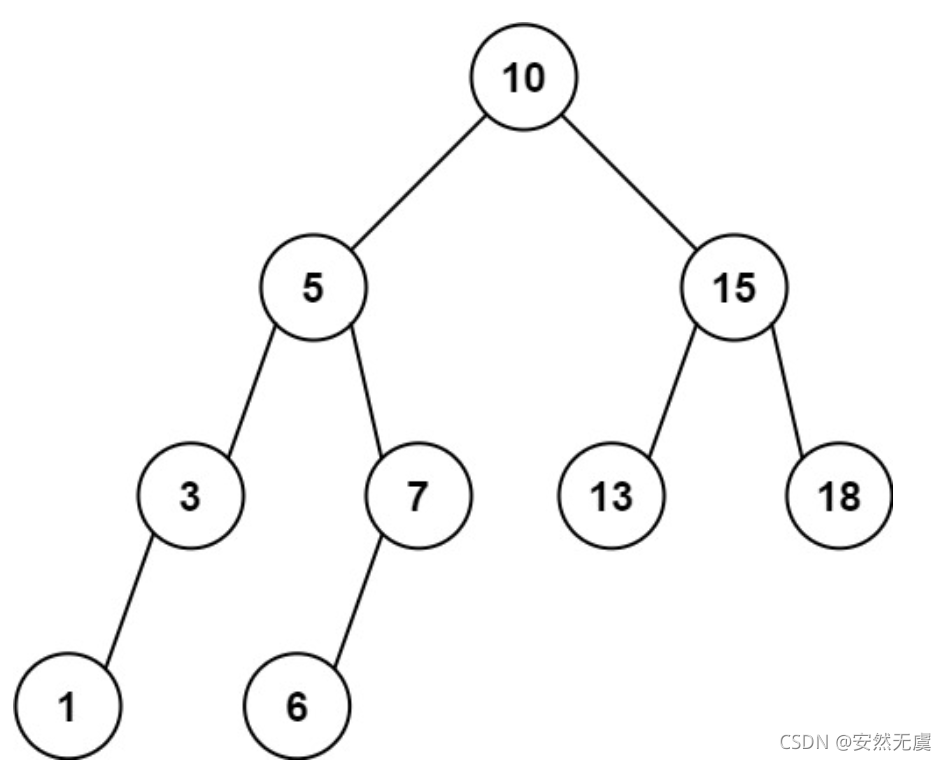
1 2	输入：root = [10,5,15,3,7,13,18,1,null,6], low = 6, high = 10 输出：23

static int rangeSumBST(TreeNode root, int low, int high) {
	//方法1：DFS
	//找递归边界（死胡同）
	if (root == null) {
		return 0;
	}
	//岔道口
	//如果根节点的值大于high，那么右子树的值一定不满足，此时只需要判断左子树即可
	if (root.val > high) {
		return rangeSumBST(root.left, low, high);
	}
	//如果根节点的值小于low，那么左子树的值一定不满足，此时只需要判断右子树即可
	if (root.val < low) {
		return rangeSumBST(root.right, low, high);
	}
	//否则根节点的值在low和high之间，则根节点、左子树、右子树这三者都要判断
	return root.val + rangeSumBST(root.left, low, high) + rangeSumBST(root.right, low, high);
}

递归

static int rangeSumBST2(TreeNode root, int low, int high) {
	//方法1：DFS
	//找递归边界（死胡同）
	if (root == null) {
		return 0;
	}
	//左子树
	int leftSum = rangeSumBST(root.left, low, high);
	//右子树
	int rightSum = rangeSumBST(root.right, low, high);
	int result = leftSum + rightSum;
	//判断根节点是否满足
	if(root.val >= low && root.val <= high){
		result += root.val;
	}
	return result;
}

岛屿数量

给你一个由 ‘1’（陆地）和 ‘0’（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例1：

输入：grid = [
  ["1","1","1","1","0"],
  ["1","1","0","1","0"],
  ["1","1","0","0","0"],
  ["0","0","0","0","0"]
]
输出：1

示例2：

输入：grid = [
  ["1","1","0","0","0"],
  ["1","1","0","0","0"],
  ["0","0","1","0","0"],
  ["0","0","0","1","1"]
]
输出：3

为了求出岛屿的数量，我们可以扫描整个二维网格。如果一个位置为 1，则以其为起始节点开始进行深度优先搜索。在深度优先搜索的过程中，每个搜索到的 1 都会被重新标记为 0,也就是说将1周围出现（上下左右）的1全部同化成0

int numIslands(char** grid, int gridSize, int* gridColSize){
    //考虑特殊情况
    if(grid == NULL || gridSize == 0){
        return 0;
    }
    int row = gridSize;//行数
    int col = *gridColSize;//列数
    int count = 0;//用于计数
    for(int i = 0; i < row; i++){
        for(int j = 0; j < col; j++){
            if(grid[i][j] == '1'){
                count++;
            }
            dfs(grid, i, j, row, col);
        }
    }
    return count;
}
 
void dfs(char** grid, int x, int y, int row, int col){
    //找递归边界（死胡同）
    if(x < 0 || x >= row || y < 0 || y >= col || grid[x][y] == '0'){
        return;
    }
    grid[x][y] = '0';
    //岔道口
    dfs(grid, x - 1, y, row, col);
    dfs(grid, x + 1, y, row, col);
    dfs(grid, x, y - 1, row, col);
    dfs(grid, x, y + 1, row, col);
}

0-1 背包问题

有n件物品，每件物品的重量为w[i], 价值为c[i]。现在需要选出若干件物品放入一个容量为v的背包中，使得在选入背包的物品重量和不超过容量v的前提下，让背包中物品的价格之和最大，求最大价值。

1
2
3

输入：物品重量：3 5 1 2 2  物品价值：4 5 2 1 3
 
输出：10

code

public class Main {
	
	static int maxValue = 0;//最大价值
	//下面四组数据可以自己设定，由于想简化题目所以在这里直接以全局变量的形式给出
	static int n = 5;//物品数目
	static int v = 8;//背包容量
	static int w[] = {3, 5, 1, 2, 2};//w[i]为每件物品重量
	static int c[] = {4, 5, 2, 1, 3};//c[i]为每件物品价值
	static int result[] = {0, 0, 0, 0, 0};

	static void DFS(int index, int sumW, int sumC, int[] list) {
		//已经完成了对n件物品的选择（递归边界--死胡同）
		if (index == n) {

			return;
		}
		//岔道口
		int[] list1 = list.clone();
		list1[index] = 0;
		DFS(index + 1, sumW, sumC, list);//不选第index件物品

		//只有加入第index件物品后未超出容量v,才能继续执行（注意这个限制条件）
		if (sumW + w[index] <= v) {
			int[] list2 = list.clone();
			list2[index] = 1;
			//注意哦，如果加入第index件物品后总价值大于最大价值maxValue时记得要更新最大价值
			if (sumC + c[index] > maxValue) {
				maxValue = sumC + c[index];//更新最大价值maxValue
				result = list2;
			}
			DFS(index + 1, sumW + w[index], sumC + c[index], list2);//选择第index件物品
		}
	}

	public static void main(String[] args) {
		int[] list = {0, 0, 0, 0, 0};
		DFS(0, 0, 0, list);//初始时为第0件物品、当前总重量和总价值均为0
		System.out.println("满足条件的最大价值为：" + maxValue);
		for (Integer integer : result) {
			System.out.print(integer);
		}
		System.out.println();

	}

}

参考文章

https://blog.csdn.net/weixin_57544072/article/details/121262172

#树