链表中的节点每k个一组翻转

描述
将给出的链表中的节点每 k 个一组翻转，返回翻转后的链表
如果链表中的节点数不是 k 的倍数，将最后剩下的节点保持原样
你不能更改节点中的值，只能更改节点本身。

数据范围： 0≤n≤2000 ， 1≤k≤2000 ，链表中每个元素都满足 0≤val≤1000
要求空间复杂度 O(1)，时间复杂度 O(n)
例如：
给定的链表是 1→2→3→4→5
对于 k = 2k=2 , 你应该返回 2→1→4→3→5
对于 k = 3k=3 , 你应该返回 3→2→1→4→5

方法一 模拟法

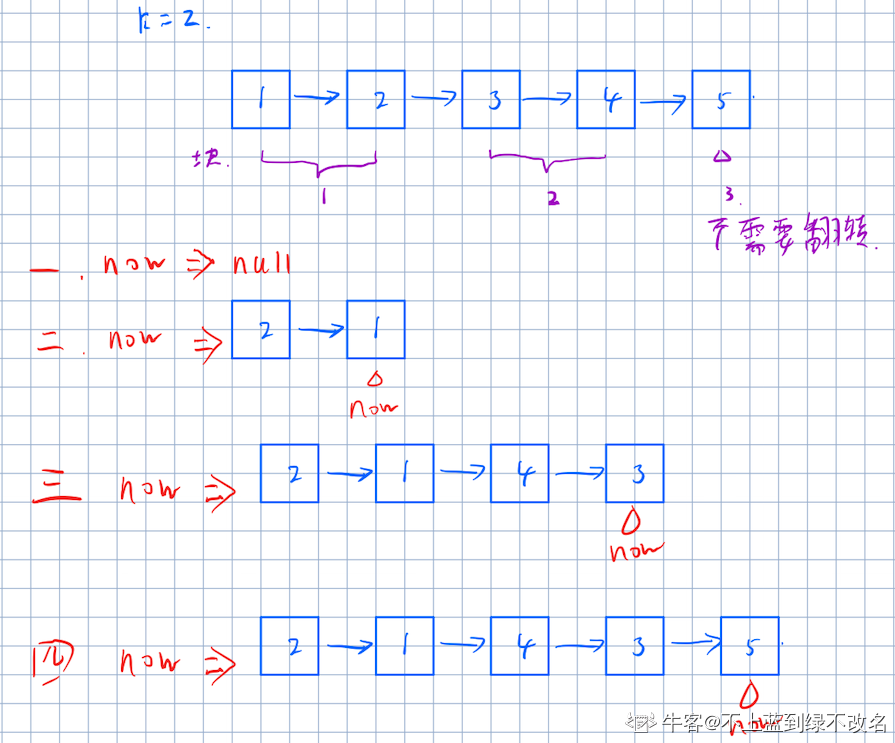
将一条链表分块分为链表长度/k块链表，如果处不尽则说明后面会有剩下的那一块是不满长度为k的。在最初的时候需要定义两个NodeList表示result(结果)和 now(当前所到达的结果链表的位置)。之后遍历块的长度，对每一个链表块进行翻转，再翻转完后将完成的链表插入到now链表的下一个，再将now链表更新到最前即可。

public class Solution {
    /**
     * 
     * @param head ListNode类 
     * @param k int整型 
     * @return ListNode类
     */
    public ListNode reverseKGroup (ListNode head, int k) {
        // write code here
        if(k <= 1) return head;
        if(head == null) return head;
        ListNode node = head;
        int len = length(head);
        head = node;
        int sx = len / k;    //分成sx块向下取整（默认向下） 因为处不尽的后面必然凑不满k个
        ListNode result = new ListNode(0);
        ListNode now = result;
        int cnt = 0;
        for(int i = 0; i < sx; i ++){
            ListNode tmp = null;
            for(int j = 0; j < k; j ++){    //将第i块的元素翻转
                ListNode bl = head.next;
                head.next = tmp;
                tmp = head;
                head = bl;
            } 
            now.next = tmp;
            while(now.next != null) now = now.next;    //将now更新到最前的一个点
        }
        now.next = head;
        return result.next;
    }
    public int length(ListNode now){    //获取链表长度
        int cnt = 0;
        if(now != null) cnt = 1;
        while(now.next != null){
            cnt ++; now = now.next;
        }
        return cnt;
    }
}

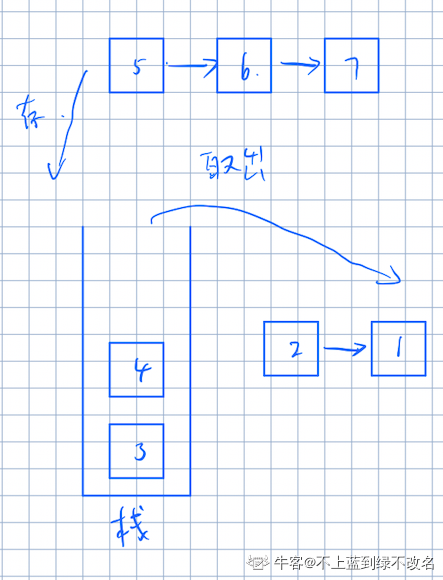
方法二 栈

和方法一一样将链表分成每段长度为k的子链表，将每个链表存入栈中，当栈中有k个元素即可一一取出，之后按取出的顺序重组链表就是这一段中翻转的链表，要注意的是处理尾部不满长度为k的链表块时直接取栈底的元素做为最后一段即可。

时间复杂度 O(n) 遍历了整个链表并且重组链表使用了时间为2n
空间复杂度 O(k) 栈中存入最大有k个ListNode

public ListNode reverseKGroup (ListNode head, int k) {
        // write code here
        if(k <= 1 || head == null) return head;
        Deque<ListNode> st = new ArrayDeque<ListNode>();    //模拟栈
        ListNode result = new ListNode(0);
        ListNode now = result;
        int cnt = 0;
        while(true){
            for(int i = 0; i < k; i ++){    //将当前链表前k个存入栈中
                st.push(head);
                head = head.next;
                cnt ++;
                if(head == null) break;
            }
            if(cnt == k){    //如果当前栈中有k个元素则一一取出存入链表
                while(!st.isEmpty()){
                    now.next = st.pop();
                    now = now.next; now.next = null;
                }
            }
            if(head == null) break;   //如果链表取完了跳出循环
            cnt = 0;
        }
        ListNode end = null;
        while(!st.isEmpty()){    //如果栈中还有剩下的就说明是最后的一块直接取栈底即可
            end = st.pop();
        }
        now.next = end;
        return result.next;
    }

方法：递归（推荐使用）

思路：

现在我们想一想，如果拿到一个链表，想要像上述一样分组翻转应该做些什么？首先肯定是分段吧，至少我们要先分成一组一组，才能够在组内翻转，之后就是组内翻转，最后是将反转后的分组连接。

但是连接的时候遇到问题了：首先如果能够翻转，链表第一个元素一定是第一组，它翻转之后就跑到后面去了，而第一组的末尾元素才是新的链表首，我们要返回的也是这个元素，而原本的链表首要连接下一组翻转后的头部，即翻转前的尾部，如果不建立新的链表，看起来就会非常难。但是如果我们从最后的一个组开始翻转，得到了最后一个组的链表首，是不是可以直接连在倒数第二个组翻转后的尾（即翻转前的头）后面，这样从后往前是不是看起来就容易多了。

怎样从后往前呢？我们这时候可以用到自上而下再自下而上的递归或者说栈。接下来我们说说为什么能用递归？如果这个链表有nnn个分组可以反转，我们首先对第一个分组反转，那么是不是接下来将剩余n−1n-1n−1个分组反转后的结果接在第一组后面就行了，那这剩余的n−1n-1n−1组就是一个子问题。我们来看看递归的三段式模版：

• 终止条件： 当进行到最后一个分组，即不足k次遍历到链表尾（0次也算），就将剩余的部分直接返回。

• 返回值： 每一级要返回的就是翻转后的这一分组的头，以及连接好它后面所有翻转好的分组链表。

• 本级任务： 对于每个子问题，先遍历k次，找到该组结尾在哪里，然后从这一组开头遍历到结尾，依次翻转，结尾就可以作为下一个分组的开头，而先前指向开头的元素已经跑到了这一分组的最后，可以用它来连接它后面的子问题，即后面分组的头。
  具体做法：

• step 1：每次从进入函数的头节点优先遍历链表k次，分出一组，若是后续不足k个节点，不用反转直接返回头。

• step 2：从进入函数的头节点开始，依次反转接下来的一组链表，反转过程同BM1.反转链表。

• step 3：这一组经过反转后，原来的头变成了尾，后面接下一组的反转结果，下一组采用上述递归继续。
  图示

• link

import java.util.*;
public class Solution {
    public ListNode reverseKGroup (ListNode head, int k) {
        //找到每次翻转的尾部
        ListNode tail = head;
        //遍历k次到尾部 
        for(int i = 0; i < k; i++){ 
            //如果不足k到了链表尾，直接返回，不翻转
            if(tail == null) 
                return head;
            tail = tail.next; 
        }
        //翻转时需要的前序和当前节点
        ListNode pre = null; 
        ListNode cur = head;
        //在到达当前段尾节点前
        while(cur != tail){ 
            //翻转
            ListNode temp = cur.next; 
            cur.next = pre;
            pre = cur;
            cur = temp;
        }
        //当前尾指向下一段要翻转的链表
        head.next = reverseKGroup(tail, k); 
        return pre;
    }
}

self

package com.company;

public class reverseKGroup {

	public static void main(String[] args) {

		ListNode listNode1 = new ListNode(1);
		ListNode listNode2 = new ListNode(2);
		ListNode listNode3 = new ListNode(3);
		ListNode listNode4 = new ListNode(4);
		ListNode listNode5 = new ListNode(5);
		listNode1.next = listNode2;
		// listNode2.next = listNode3;
		// listNode3.next = listNode4;
		// listNode4.next = listNode5;

		ListNode result = reverseKGroup(listNode1, 2);
		System.out.println(result);
	}

	public static ListNode reverseKGroup(ListNode head, int k) {
		if (head == null) {
			return null;
		}
		ListNode dummyNode = new ListNode(-1);
		dummyNode.next = head;

		ListNode pre = dummyNode;
		ListNode cur = head;

		ListNode left = null;
		ListNode right = null;

		while (cur != null && cur.next != null) {
			left = cur;
			int i = 0;
			for (; i < k - 1; i++) {
				if (cur.next == null) {
					break;
				}
				cur = cur.next;
			}
			if (cur.next == null && i < k - 1) {
				break;
			}
			right = cur;

			cur = cur.next;
			right.next = null;

			revert(left);
			pre.next = right;
			left.next = cur;
			pre = left;
		}

		return dummyNode.next;
	}

	public static ListNode revert(ListNode head) {
		ListNode pre = null;
		ListNode cur = head;
		while (cur != null) {
			ListNode cur_next = cur.next;
			cur.next = pre;

			pre = cur;
			cur = cur_next;
		}
		return pre;
	}

	public static class ListNode {
		int val;
		ListNode next = null;

		ListNode(int val) {
			this.val = val;
		}
	}
}